鉄でつくられた船が浮く理由については、『船はどうして浮くの?』でカンタンに説明しました。
物体が押しのけた分の水の重さが浮力となるのでしたね。これをアルキメデスの原理といいます。
では、どうして押しのけた分の水の重さが浮力となるのでしょうか。アルキメデスの原理を物理的に理解していきましょう。
①質量と重量のちがい
これから浮力の原理を理解するにあたって、質量と重量のちがいを理解しておく必要があります。
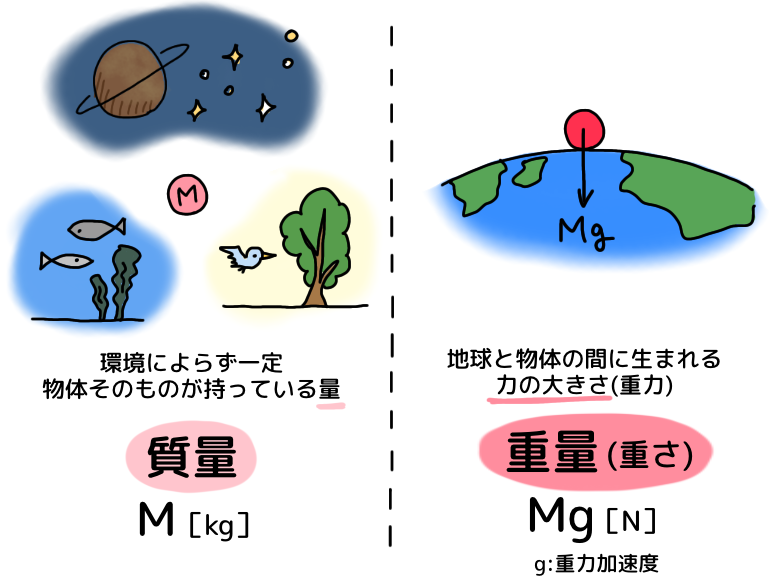
質量は、物体そのものが持っている量のことです。これは、水中にあったり宇宙にあったりしても変わることのない量です。通常、質量を意味する”mass”の頭文字をとって、Mまたはmで表します。
質量の単位は[g]や[kg]です。
一方、重量は、地球(惑星)と物体の間にうまれる力の大きさ、すなわち重力のことです。重さ、というのも重量のことを差します。重量は、質量Mに重力加速度gをかけ算したもの、Mgで表します。(gは重力を意味する”gravity”の頭文字)したがって、月に行くと重力は6分の1になるため、重量も6分の1に変化します。※体重計で測っている体重は●●kgなどと言っていますが、質量ではなく重量だということになります
重量の単位は[N](ニュートン)です。
②密度と単位重量のちがい
物体を浮かべる液体のことをこれまで「水」と呼んでいましたが、正確には「流体」と呼びます。物体を浮かべる流体は、真水かもしれないし、海水かもしれないし、はたまたオレンジジュースかもしれません。それぞれ密度が異なります。
はじめに(浮力)=(物体が押しのけた分の水の重さ)と書きましたが、”流体の重さ”は流体の密度によって変わってきますよね。つまり、浮力には流体の密度が関係することになります。ここで密度について、①をふまえて考えてみましょう。
密度は、ある体積あたりの流体の「質量」のことです。ここではρで表します。
単位重量は、ある体積あたりの流体の「重量」(力の大きさ)のことで、密度ρに重力加速度gをかけたものになります。ここではγで表します。(γ=ρg)
物理では物体にかかっている”力の大きさ”のつり合いを考えるため、このあと”密度”ではなく”単位重量”のほうを使います。
③静水圧とは
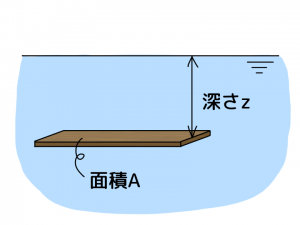
静止した水の中で物体が受ける圧力を「静水圧」といいます。簡単に考えるために、平らな板が深さzのところに浮いているとします。板の面積をA、大気圧をP0、水(流体)の単位重量をγとします。
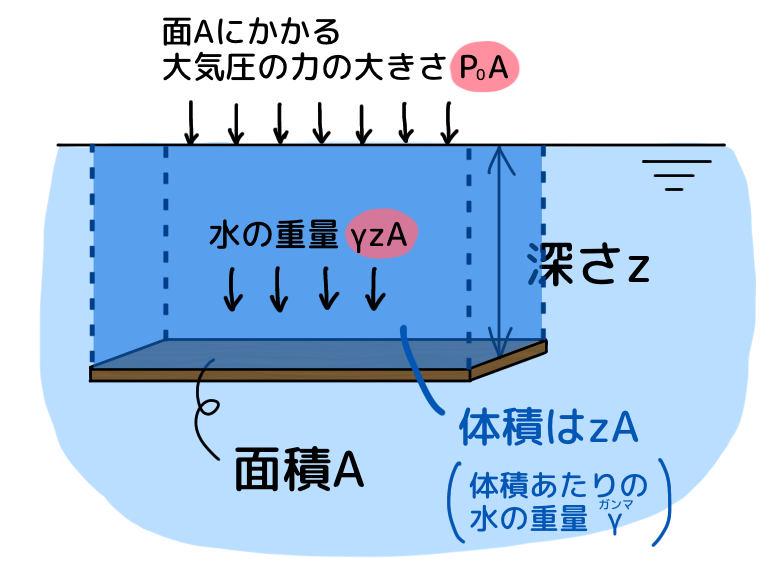
面積Aの板にかかる下向きの力F’は、大気圧の力の大きさ+板の上にある水の重量 の合計になります。大気圧(圧力)は単位面積あたりの力を差しているので、面積Aあたりにかかる大気圧の力の大きさはP0・A。板の上にある水の体積はz・Aであり、単位重量がγなので、水の重量はγ・z・A。
つまり、面積Aの板にかかる力F’は、F’ = P0A + γzA となります。
これを単位面積あたりに換算するなら全体を面積Aで割って、
p’ = F’/A = P0 + γz となります。この静止した水中で単位面積あたりに働く力を「静水圧」と言います。
大気圧P0が含まれているものを「絶対圧力」と呼び、大気圧を基準(P0 = 0)として考えた相対圧力のことを「ゲージ圧力」と呼びます。
ゲージ圧力pは、p = γz であり、同じ流体の中にある物体が受ける静水圧は物体の沈んだ深さzにのみ関係することがわかります。
深ければ深い位置にあるほど、大きな静水圧がかかることになりますね。
④静水圧の重要な性質
静水圧には重要な性質が2つあります。
・静水圧は面に対して直角にはたらく
・静止した水中の1点における静水圧の強さはすべての方向に等しい
これの証明は省略します。気になる方はコメントください。
→コメントをいただきましたので以下に解説します。
そもそも「圧力」は「面に対して垂直に働く力」がその定義なので、静水圧も水中の物体の面において垂直に働く力となります。どんな力が働いていても、面に対して垂直方向と水平方向に分解することができ、分子レベルで考えると押し合い(作用反作用)が働くのは垂直方向成分のほうであることがわかるかと思います。
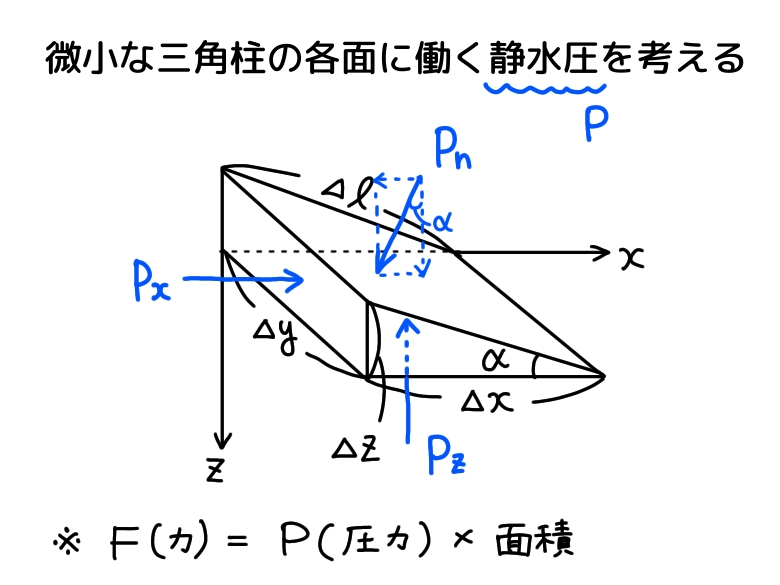
特に証明したいのは2こめの「静止した水中の1点における静水圧の強さはすべての方向に等しい」です。水中に静止した微小な三角柱があるとします。Δ(デルタ)記号は”微小な、極めて小さい”という意味です。各面に静水圧Px、Pz、Pnが働いているとします。
圧力は面積あたりの力だったので、力を出すには圧力×面積になります。x軸方向、z軸方向における力のつりあい式をたてます。
x軸方向:
Px(ΔyΔz)-(PnΔyΔl)sinα=0
z軸方向:
(PnΔyΔl)cosα-Pz(ΔxΔy)+1/2ρgΔxΔyΔz=0 (←最後の項は物体の重量)
ここで図より、Δx=Δl cosα、Δz=Δl sinα であることがわかりますので、↑のつりあい式に当てはめると、
x軸方向:
Px(ΔyΔl sinα)-(PnΔyΔl)sinα=0 より
Px=Pn が得られます
z軸方向:
(PnΔyΔl)cosα-Pz{(Δl cosα)Δy}+1/2ρg(Δl cosα)Δy(Δl sinα)=0 より
Pn cosα-Pz cosα+1/2ρg Δl sinα=0 となり、
ここでΔl→0 へ収束させていくと(三角柱を1点に縮めていくイメージ)
Pn=Pz が得られます
すなわち、Δl→0においてPx=Pz=Pn となりました。この関係式にαは含まれていないため角度は任意、つまり静止した水中の1点にかかる静水圧はすべての方向において等しいことがわかります。
⑤アルキメデスの原理の導出
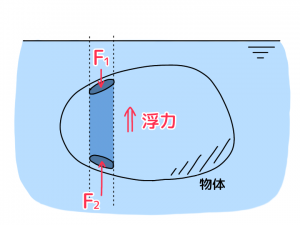
③と④より、水中の物体は水深が浅い面よりも深い面のほうが大きな力を受けるため、(下面にかかる力)ー(上面にかかる力)の差分だけ上向きに浮力として力がはたらくことがわかります。
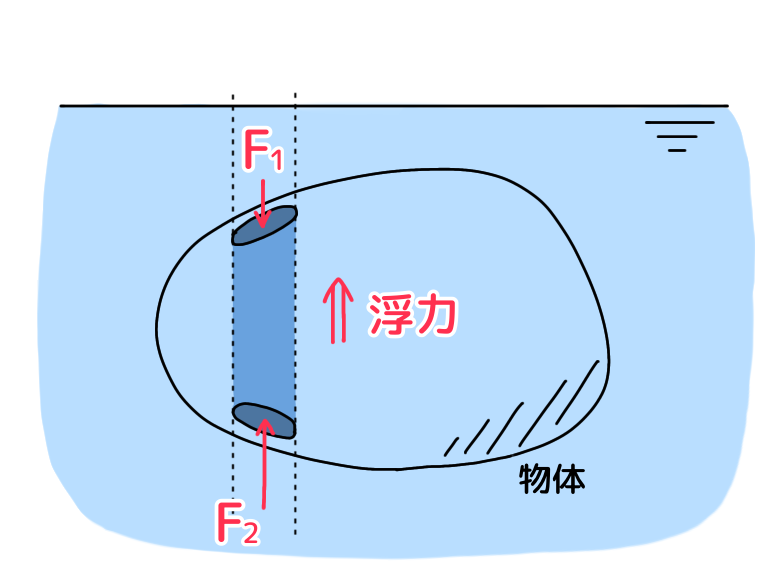
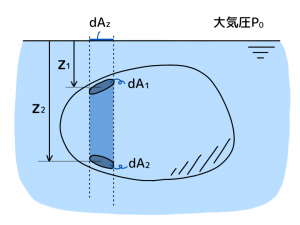
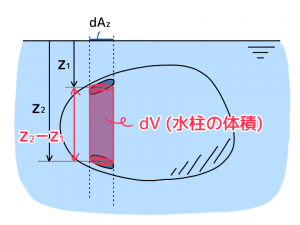
水面にごくわずかな面積dAzをとり、これを底面とする水柱を考えます。水柱が物体を貫く両端の面積をdA1, dA2とし、それぞれの深さをz1, z2とします。
(上向きにかかる浮力dF)=(下面にかかる力F2)-(上面にかかる力F1) にあてはめて考えます。
③より、面Aにかかる力FはF = P0A+γzAだったので、
F1 = P0・dAz+γ・z1・(dA1・cosθ1)
= P0・dAz+γ・z1・dAz
F2 = P0・dAz+γ・z2・(dA2・cosθ2)
= P0・dAz+γ・z2・dAz
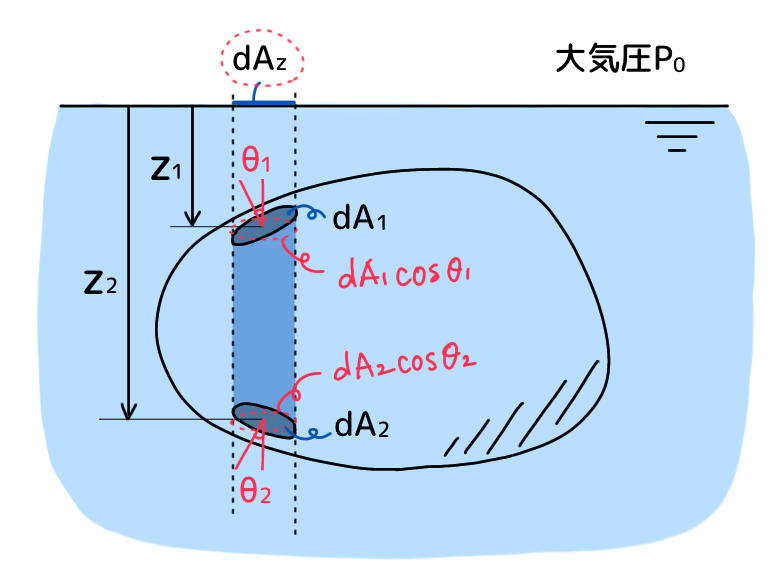
※静水圧は力と直角な面で考える必要があるため、dA1, dA2にそれぞれcosθ1, cosθ2をかけて面を水平方向に修正。下図より結局のところdAzに等しくなります。
浮力dF = F2-F1
= {P0・dAz+γ・z2・dAz} - {P0・dAz+γ・z1・dAz}
= γ・z2・dAz - γ・z1・dAz
= γ(z2 - z1)dAz
= γdV
dF = γdV
これは今、《微小な体積にかかる微小な浮力の式》となっていますので、物体全体へ展開する(積分する)と、
F = γ∫dV = γV
これがアルキメデスの原理です。
浮力Fは水中の物体の体積Vに単位重量γをかけたもの、つまり物体が排除した体積分の流体の重さに等しくなります。
γ = ρgですので、
F = ρgV とも書けます。中学や高校で習う浮力の公式はこの形のほうが多いかもしれませんね。
以上、なにかご不明点やご指摘がございましたらコメント欄またはお問い合わせよりメッセージお願いします。

④の証明お願いします!
コメントありがとうございます。④に追記しました。